Save more fuel than Lando Norris: How to drive an F1 car efficiently

Ever wondered how Lando Norris manages to save fuel while winning races? In our previous article, we explored the benefits of starting an F1 race with a light fuel load and mastering fuel-saving through the race. While this strategy is straightforward for Canopy/Michelin’s laptime simulation to identify, it has taken Lando Norris years to perfect, always requiring guidance from simulations to execute flawlessly.

In this article, we’ll uncover the magic behind how dynamic simulations can discover the fastest solutions and what these strategies look like in practice.

The Challenge

Dynamic Lap formulates the problem as a giant numerical optimisation:

-            Inputs: vary brake, throttle, steer, racing line position.

-            Objective: quickest possible laptime within a fuel constraint while adhering to car physics.

Fuel saving involves just two additional parameters: a fuel map showing consumption for different RPM and throttle positions, and a fuel target added to the solver’s objective function. The solver then determines the fastest way to drive while meeting the fuel target. The real challenge is understanding why it chose a particular strategy.

Decoding the Optimal Fuel Strategy

The graph below compares a flat-out lap with one targeting a 0.25kg fuel saving. Dynamic Lap can produce extra output channels, Secondary Lap Sensitivities (SLS), to aid understanding. These sensitivities show how much lap time the car would gain with a unit change in a parameter for every meter around the track.

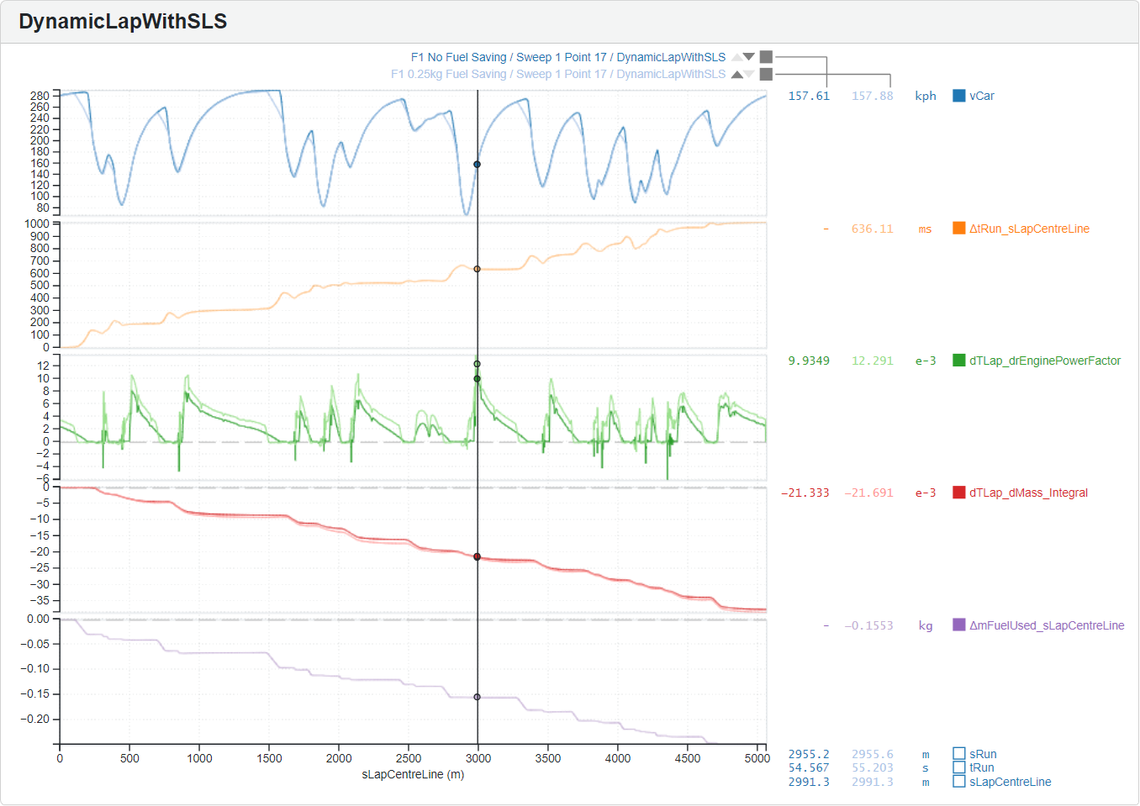
For instance, at the cursor position, doubling the engine power for just one meter could improve lap time by 9.9 milliseconds (green line). However, such a significant power increase would likely cause the tires to lose traction. To get a more realistic estimate, you can divide this value by 100 to see the effect of a 1% power change. Although SLS channels are technically valid only for small changes, they effectively highlight the most beneficial points for adding or removing power.

Full Throttle on Corner Exit

On corner exits, after the racing line straightens and the car gains enough speed to no longer be traction-limited, applying full throttle yields the greatest benefits [as shown by the biggest spike in the dTLap/drEnginePowerFactor SLS channel above, in green]. This shatters the Fast and Physicless movie myth of pressing the NOS button towards the end of a drag race. Instead, drivers should boost soon after reaching full throttle to maximise acceleration, and to carry this benefit forward for the majority of the straight.

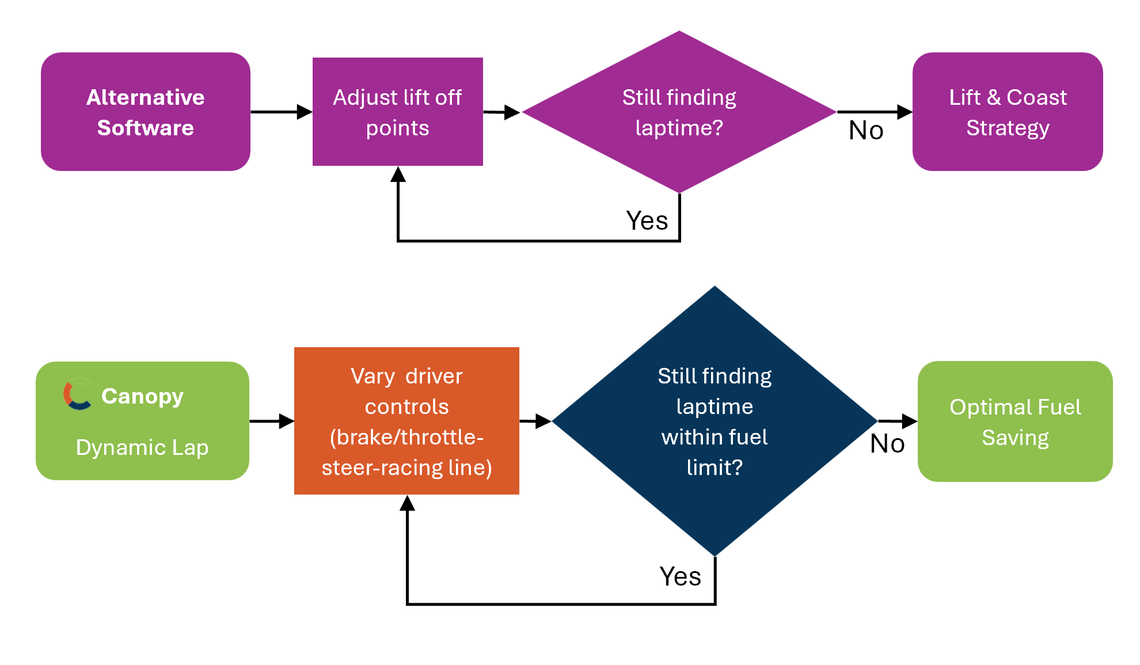
Comparing Software Approaches

Dynamic Lap acts like a big-picture manager: “Save this much fuel, and I’ll let you decide how.” Other simulations are micro-managers: “Work exclusively on my lift and coast concept.”

Why It Matters

Dynamic Lap’s approach has two distinct advantages:

1. Innovation: It can find additional strategies we had not considered, like taking a different racing line (see image below) or lifting slightly in high-speed corners where fuel is wasted due to tyre slip.

2. Adaptability: It can easily adapt to other problems by including them in the objective function, such as brake saving, tyre optimisation, thermal constraints, or electrical energy management.

Conclusion

Lift and coast is a well-established motorsport strategy for conserving fuel with minimal impact on laptimes. Secondary lap sensitivities reveal why this method is effective: power sensitivity is at its lowest when the car is about to brake. Canopy/Michelin’s lap time simulation can discover this strategy without prior knowledge, optimising driver inputs to find the minimum lap time within a fuel constraint.

Moreover, Dynamic Lap’s approach offers a significant advantage. It can uncover numerous additional opportunities for fuel savings that pre-programmed algorithms might miss. This example merely scratches the surface of how Dynamic Lap leverages its flexibility and creativity to boost performance, ultimately leading to a faster car on the track.