F1 Goes To Indy
DECEMBER 13, 2019
The idea of an F1 team going to compete in Indianapolis is hardly a new one. The most recent example being McLaren’s disastrous foray in 2019, which resulted in an ignominious failure to qualify. However, what few people have asked is “what would really happen if an F1 team took their car to Indianapolis?”. This used to happen in the form of the USA Grand Prix, up until 2007, but the course back then only used a small section of the banking; we’re interested in how an F1 car would perform in an oval race.

Indianapolis, the nexus of oval racing.
Well, in the virtual world we can do whatever we please, so let’s find out. One of the default cars available on the Canopy Platform is a fairly good impression of an F1 car. What we’d like to do is see how well this car would do around Indianapolis, while staying within the F1 regulations. If we run this around Barcelona we get a lap time of 1:17.427, which is in the vicinity of the fastest lap at the 2019 Spanish Grand Prix (1:18.492).
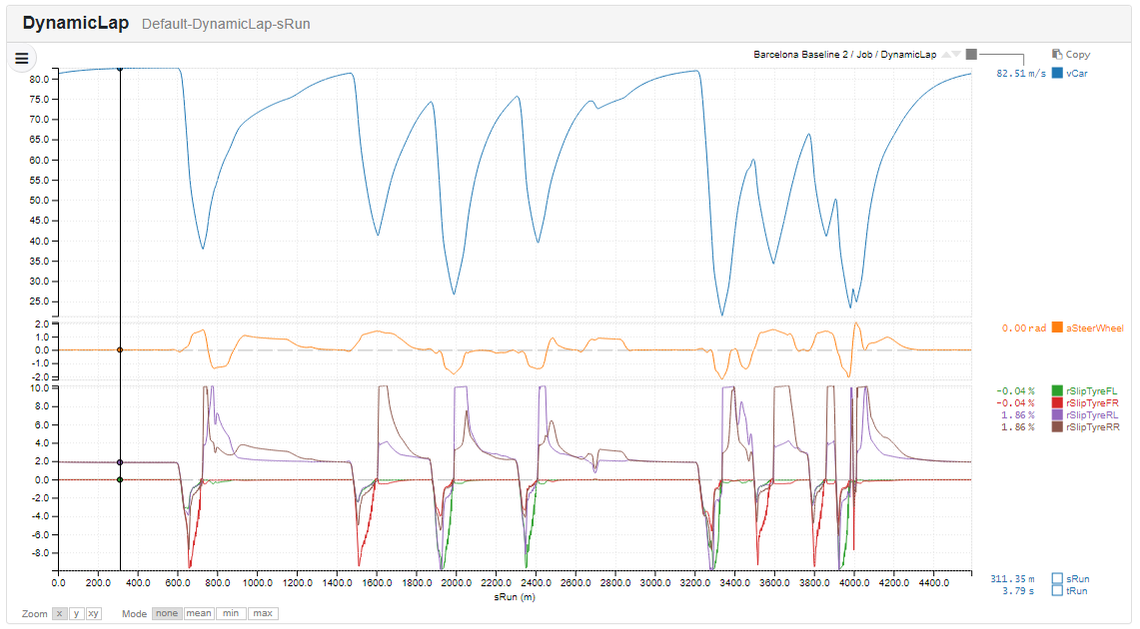
A baseline lap of the “Canopy F1 Car” around Barcelona. The Spanish Grand Prix track is a classic benchmark track, with a mix of high, low and medium speed corners which test all aspects of a car’s performance.
Indianapolis is, to say the least, not much like Barcelona. It consists of only 4 left hand turns, each of which enjoys the benefits of favourable track camber. Each corner is, by F1 standards, a wide sweeping turn which does not challenge the limits of the F1 car’s grip.
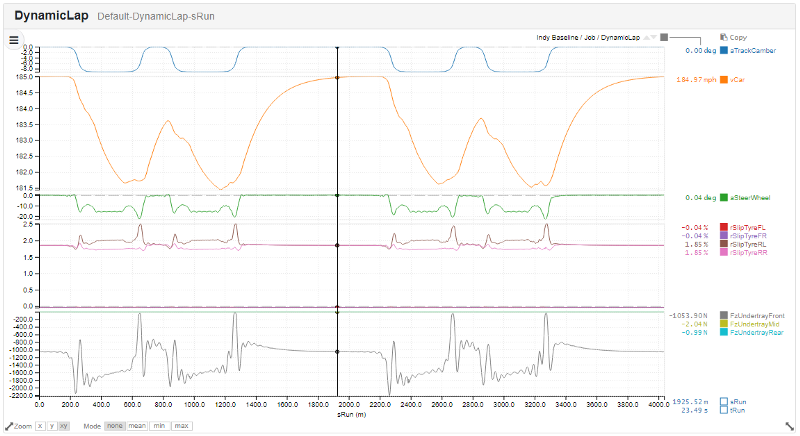
The Results of a DynamicLap simulation of an F1 car at Indianapolis Motor Speedway.
The results of this simulation are pleasingly clean; there are a few wiggles in the vCar trace as the car has to cope with simultaneous changes of curvature and track banking at corner exit and entry. The lap time is 49.19s which corresponds to a lap speed of 183.26mph (to use Indy Car’s favourite measure of competitiveness). This, frankly, would get you laughed out of the state of Indiana, and probably never allowed back. In 2019, Spencer Pigot was fastest in the qualifying time trials at a dizzying 230.083mph.
So, can our F1 car do any better, assuming that we keep it within the rules of F1, and don’t cheat by increasing the engine power factor by vast amounts? The telemetry from our first lap includes one big fat clue to why our F1 car is slow — the undertray (or plank) is dragging along the ground for the entire lap. In F1, the plank tends to touch down near the end of the straights as downforce reaches sufficient levels to move the suspension and squash the tyres sufficiently. Dragging the plank along slows the car at the end of the straight, but this is a fair exchange for getting the front of the car low at mid-corner (low front ride heights improve downforce over the whole car).
Raising the front ride height by 5mm gets the plank clear of the ground on the straights, but the effects of compression around the corners requires a further 3mm of ride height increase to avoid touching down on the banking. This yields an improvement to a moderately better 187.458mph.
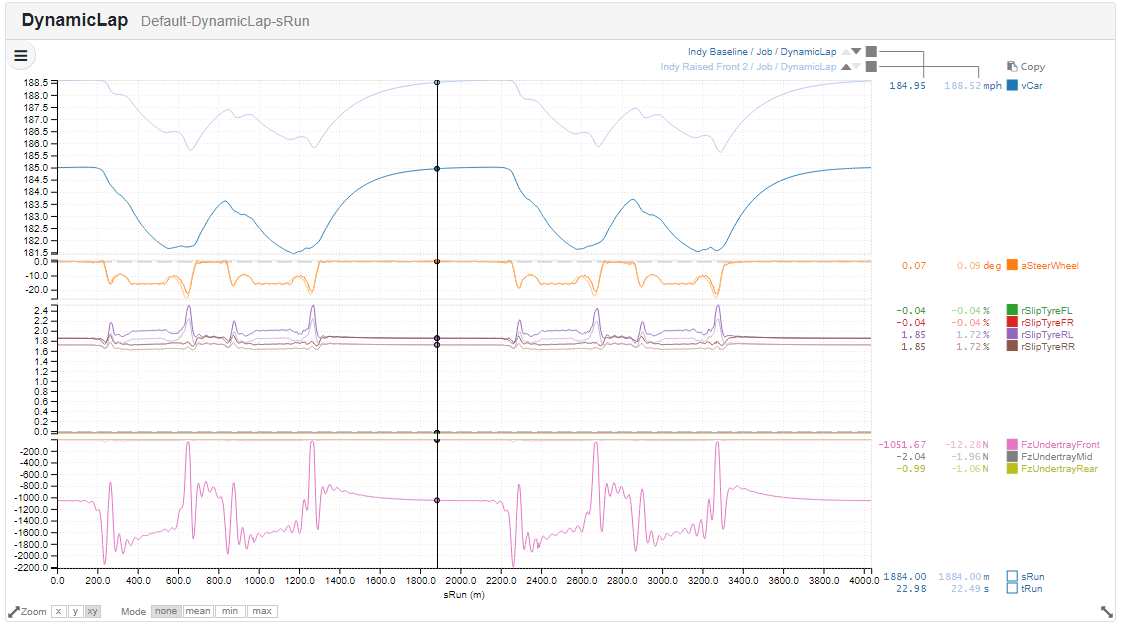
A comparison of the performance of our baseline car, which drags the plank around the entire track, and the performance of a modified car with a raised from ride height.
We have, however, missed the point here. If we go back to Barcelona we can plot localised sensitivities to aerodynamic downforce. These are a fantastically powerful piece of technology, unique to Canopy, which enable us to understand the sensitivity to a change in any car parameter — pinpointed to the location on the track where the performance improvement originates. The chart below shows the sensitivities to overall downforce and drag around Barcelona.
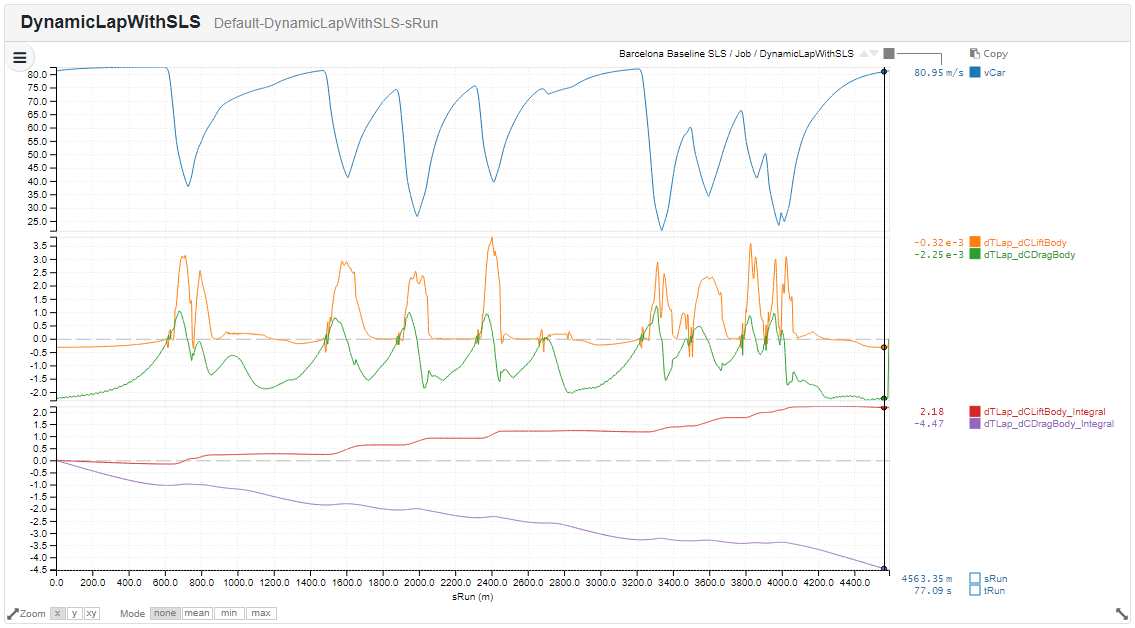
SLS sensivities for aero lift coefficient and aero drag coefficient around Barcelona.
Overall we gain 0.0218s per “point” of downforce, but lose 0.0447 for every point of drag. This is the “isochronal ratio” of the car; the ratio between increasing downforce and increasing drag which yields no lap time change; in this case 2.05. To no one’s great surprise increasing lift coefficient is very helpful going through corners (F1 engineers refer to lift and downforce interchangeably; although this is confusing, it always refers to a force acting to stick the car to the track). Increasing drag is generally unhelpful, unless you are trying to slow down. Somewhat more surprising is that increasing lift is unhelpful along the straights; it turns out that additional downforce causes higher rolling resistance in the tyres.
It’s easy to see where this is going; at Indy both lift and drag are damaging to our performance!
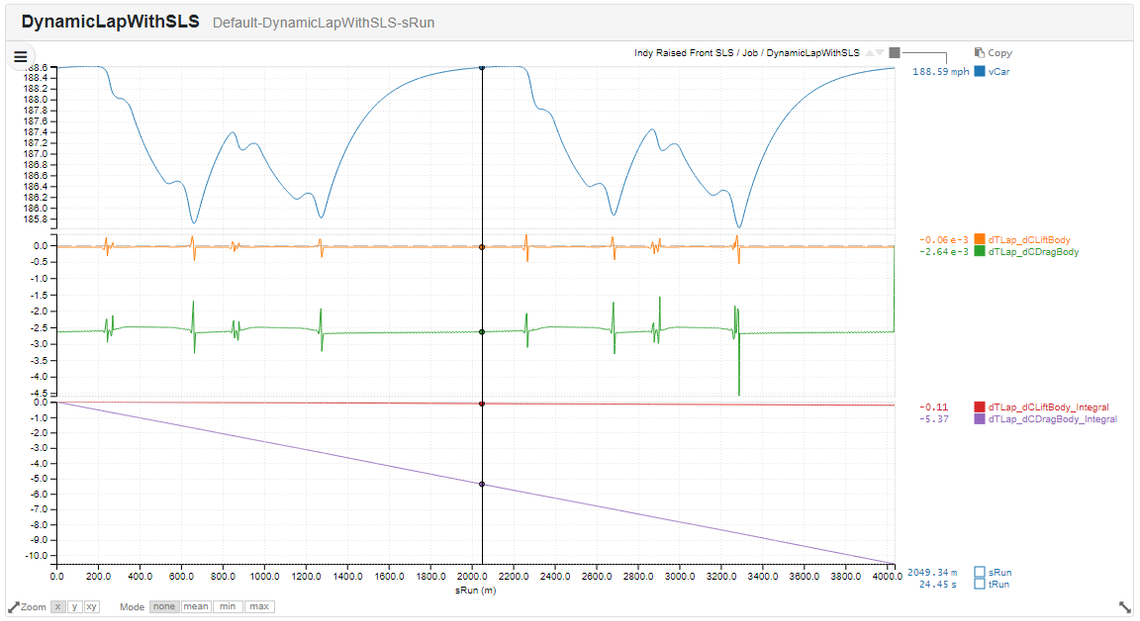
Indianapolis; both downforce and drag are damaging to performance. Time to start attacking all those bits of carbon with a big saw!
So, if we really want our F1 car to get around Indy quickly we can arrive at the following easy conclusions:
Lose as much drag as possible. We can do this by either fitting different rear wings and different bits of twisted carbon elsewhere on the car, or by adjusting the setup of the car such that the body is presented in such a way that drag is minimized.
The loss of downforce that comes with getting rid of drag won’t hurt.
If we can do a good enough job of 1&2, at some point we’ll go so fast we’ll take the engine over the top of its torque curve, so we’ll probably need some new ratios in the gearbox.
The step by step approach to finding performance here would require a variety of educated guesses, and a large amount of iteration. The relationship between gear ratios, aero setup and mechanical setup is complex so the chances of getting the best answer out is very low, at least within the tolerance for iteration of most engineers.
We can shortcut this by simply using the Canopy Platform to fire off a large exploration. I’ve created an exploration which explores:
Varying downforce and drag in the ratio 3:1; this is fairly typical of what can be achieved by changing aero setup.
Varying front and rear ride heights over the achievable setup ranges for this car (30–50mm front, and 100–130mm rear).
Varying the entire set of gearbox ratios between 90% and 130% of their baseline values.
The Canopy Platform will randomly choose 1,000 car setups among these possibilities, and run appropriate simulations. We can then intelligently explore the results. After 25 minutes, the results are ready for us. The first output of this exercise is the “parallel coordinates plot”. Each of these 1,000 lines represents a single lap time simulation. The four left most columns correspond to the parameters we varied in the exploration, and the two right most show the two outputs we care about in this case: lap time and maximum achievable straight line speed. This plot can be manipulated in various ways to get a feel of how performance varies with the setup parameters.
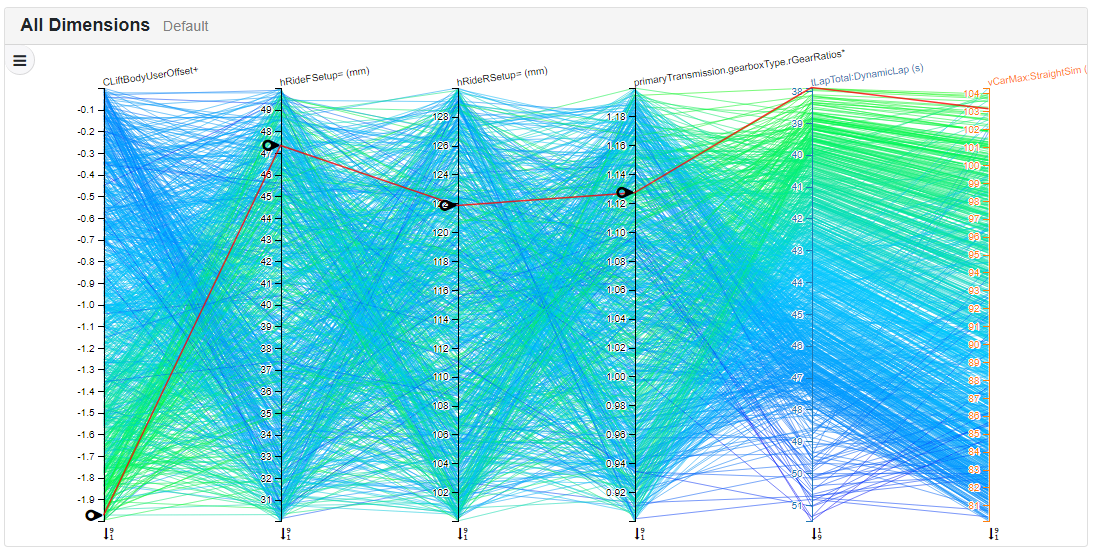
A parallel coordinates plot, showing the outputs of our exploration.
This plot make is pretty clear that there is a strong correlation between losing lift and drag and going fast; so far so unsurprising. Although the parallel coordinates plot is a nice way to explore data, we need a different view to pick out the effects of ride heights and gear box ratios. Behind the scenes the Canopy Platform has fitted a set of functions (high dimensional surfaces) which map from the input variables to each of the outputs. We can then plot slices through this surface to understand the “performance landscape”.
These plots look fairly smart statically, but nothing compares to using them live; as each slider on the x-axis is adjusted, all the other plots simultaneously update.
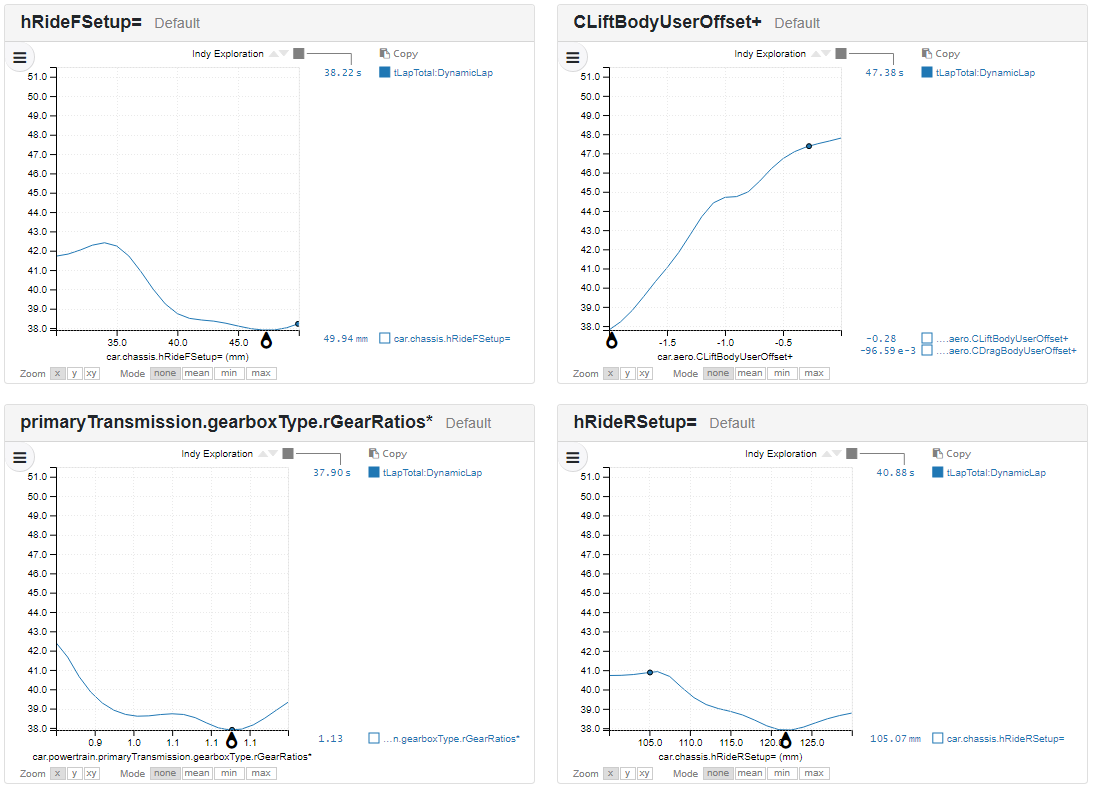
Slices through a hypersurface fitted to the results from the 1,000 simulations in our exploration. All the variables show a clear optimum value.
This set of viewers shows us that losing lift and drag is unequivocally good, but in all other variables there are nice clear optima. The “double dip” shown in the gear ratio plot corresponds to whether the car uses 7th or 8th gear along the straights. The ride heights also show clear optima; the rear ride height is at an unremarkable 122mm, while the front ride height is a very high 47mm.
So if we go back to run a single experiment with these optimum settings what do we get?
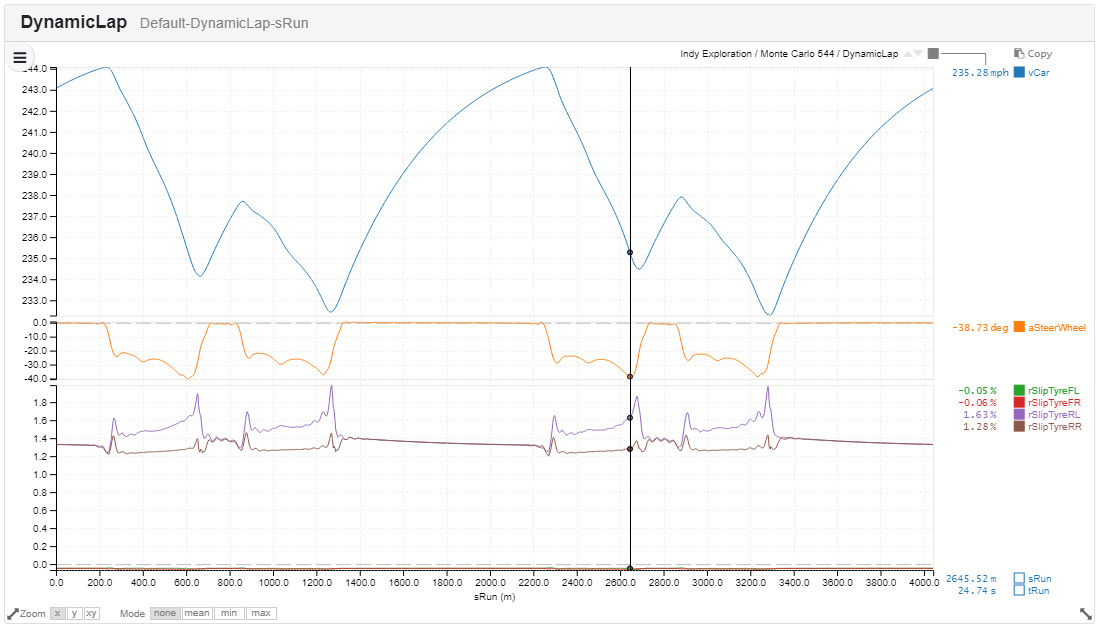
A new lap around Indy, with modified ride heights, gear ratios and aero setup.
This is transformed since the car which we took from Barcelona. The average speed: a frankly unbelievable 238.653mph!
So would a modified F1 car really go faster around Indy than the fastest Indycars? The simple answer to this is that it almost certainly wouldn’t; I really don’t think it’s possible to shed as much drag as we have here and remain within legal in F1. In fact, it may not even be possible to remove this much drag from an F1 car at all.
However, what we have done is shown that we can use the Canopy Platform to take a car setup for one circuit to another circuit, rapidly understand what drives performance, then find our way to a much improved setup.
Based on this analysis you may ask “why do Indy Cars have wings at all, if shedding lift and drag is such a good idea”. This gets to the heart of a false simplification we’ve made in our analysis above; as we try to find more and more downforce, it becomes less and less efficient (i.e. it comes with more and more drag). An Indy car produces a relatively small amount of downforce; you don’t need much at Indy, but it can produce this downforce for very little induced drag. We, on the other hand, assumed that the relationship between drag and downforce would remain constant across our search range. In reality we would find that near the real operating range of an Indy car, downforce is indeed beneficial.
If you would like to find out how to exploit our unique technology to make your real Indy car go faster, do get in touch via hello@canopysimulations.com.